Journal of Psychological Science and Research

The objective of the present study was to explore and describe the influence of a proposal that returns to Problem Based Learning for the application arithmetic principles in the solution of problems in sixth grade students of primary education. Eighty-six of sixth grade students participated with an average age of 11.0 years. The intervention strategy was carried out in nine sessions lasting approximately one hour each. The results in general, do not show statistically significant differences in the performance of the execution in the resolution of problems between pre-test and post-test conditions, however, it was observed through the students' report that they had experienced knowledge acquisition based on the content of the intervention.

Keywords: Problem solving, Problem based learning, Arithmetic, Primary school

Mathematical knowledge is a skill that is present from a very early age,^1-3 develops according to chronological age and with school learning Berch⁴ defines mathematical knowledge as a set of skills such as awareness, intuition, recognitions, knowledge, experience, ability, desire, sensation, explanation, processing, conceptual structure and mental schemes of the number and its applications.

Within the educational context the pedagogical implications are on the development of mathematical skills are much more complex than intuition to quantitative elements;^4,5 In other words, it must be a way of thinking that involves and connects all aspects of mathematics teaching and learning, putting into practice different constructivist strategies that involve paradigms related to the theoretical conception and the empirical findings reported so far⁴ giving meaning and functionality to the knowledge that students will learn, an example of this is the resolution of contextualized arithmetic problems.

The academic problems that prevail in the Mexican educational system today are a function of teaching practices and various forms of studies that are put into practice in the space of cultural exchange called the classroom.

At all educational levels there is an overwhelming use of didactic experiences focused on information transmission methods (e.g. exhibition, demonstration, use of visual aids such as slides) and the follow-up of routines in practical situations, in which the role that the students play is exclusively of receivers of information without the sufficient context (conceptual and social), nor the necessary questioning for the formulation of problems and their resolution.⁶ That is, the teaching methods and the way of evaluating knowledge lead students to perform rote and information retention exercises,⁷ instead of the investment of cognitive resources to reason, understand and master knowledge.

One of the teaching-learning methods applied in various areas of knowledge, specifically in population segments of upper secondary and higher education is Problem Based Learning (PBL), which is defined as the knowledge acquisition strategy that impacts the development of significant skills, aptitudes and attitudes.^8-12 The methodological forms of PBL include the integration of a small group of students who, with the facilitation of a tutor, will analyze and solve a problem selected or specially designed to achieve certain learning objectives.^9,10

Although a good memory of the facts, the definitions and even the formulas is enough to be successful in basic-level subjects, including mathematics, the problems offered in textbooks encourage students to repeat the pattern of responses guided by memory or in the worst case by the obvious; That is why, the ABP brings together methodological tools capable of facilitating the acquisition of the objectives proposed for academic training.^9,12

The PBL is a constructivist approach¹² based on the analysis, solution and discussion of some problems, thanks to the fact that its structure and the problem-solving process are always open;^8,10,11 therefore, it encourages conscious learning and systematic group work in a collaborative learning experience.¹³ The main objective is the comprehensive development of the student, combining the acquisition of their own knowledge as well as involving skills, attitudes and values. This paradigm integrates theory and practice, and applies the knowledge and skills that are developed in its execution.¹³

Some authors^12,13,15-18 they consider the APB as a fundamental piece for the mathematics teaching-learning process since they point out that instruction in mathematical problem solving is a fundamental axis in the development of mathematical knowledge at any level, including primary education. All those who use mathematics will have to solve some type of problem at a certain point; therefore, the development of problem solving should be part of the school curriculum. There is little evidence of the application of PBL in the teaching of mathematics in basic education at the primary level.

Martínez and collaborators¹⁹ and Díaz and Bermejo²⁰ formulated a couple of studies in which the problem situations are inscribed based on a mathematical nature in different contexts.

The results in general showed that initially the students solved the problems mechanically using known algorithms; Later, in the course of the didactic experience, the students improved their attitude and performance, in addition to the fact that in the final evaluation the students approached the task with a much greater degree of flexibility of reasoning and interest. In the same way, it was found that the evolutionary trend frames the performance of the students, since the behavior of the participants improves significantly as the academic degree progresses. It was also found that there is a succession of abstraction from the concrete to the abstract, and that an influencing factor is the verbal aspect, being less favorable for students from a rural context. Finally, it was confirmed that the unknown significantly affected the mathematical behavior, since it is easier to solve with the final unknown than the initial one.

Based on what has already been argued, the objective of this study was to describe the influence of a psychopedagogical intervention derived from Problem Based Learning within the use and application of arithmetic in everyday situations in sixth-grade primary school students.

A mixed type study (quantitative-qualitative) was carried out, due to the form of data collection and analysis; quasi-experimental due to the design used (pre-test/post-test); descriptive and transversal due to its epistemological order of knowledge and the time elapsed within the planned intervention.

Participants
A convenience sampling was used in which 61 students enrolled in the sixth grade of primary education participated (N=30 women; N=31 men), with an average age of 11.0 years. In good general health, and without any extra requirement for inclusion in the study.

Material
A workbook constructed for psychopedagogical intervention based on the PBL methodology was used. Its content was made up of:

1. a. Presentation and welcome, a section that had the purpose of familiarizing the student with the intervention
2. b. Set of arithmetic operations accompanied by the conceptual definition of each one (eight additions, eight subtractions, eight multiplications and eight divisions)
3. c. Conceptualization of a problem, that is, what are its elements and some examples
4. d. Eight problems grouped by initial or final unknown (two of each arithmetic operation)
5. e. Two logical reasoning exercises
6. f. An exercise to generalize the use of arithmetic knowledge in everyday activities

Instrument
A paper and pencil-type instrument with an open structure was constructed, comprising a student identification section and a total of eight items. The first five questions were focused on posing contextualized arithmetic problems, which were taken from the study by Martínez and collaborators (2009), adapting some linguistic terms to the sociocultural context of the students. On the other hand, the position of the unknown within the problem was modified, retaking the initial and final unknown parameters used by Díaz and Bermejo (2010). The remaining questions were about the perception and evaluation that the students had as an experiential experience of the intervention.

Procedure
The study consisted of nine sessions, divided into an initial evaluation session, seven psychopedagogical intervention sessions and a final evaluation session. The evaluation sessions lasted approximately one hour, while the intervention sessions lasted an hour and a half, being carried out with 90% attendance by the students.

The initial evaluation was carried out in the first session, carrying out the application of the investigative instrument on contextualized arithmetic problems.

The intervention comprised seven sessions, held once a week, in which the following activities were addressed respectively:

1. a. The first activity consisted of addressing the concepts: a) mathematics, b) arithmetic, c) arithmetic operation, d) addition, e) subtraction, f) multiplication, and g) division through 15 operations exercises. Using the number line as the main source of support.
2. b. In the second activity, there was a general review of arithmetic principles and abstract thinking, as well as some association exercises on the use of mathematics in the students' daily lives.
3. c. The third activity was carried out in teams of five members; The objective of the activity was to develop both individual and group skills in problem solving, developing and exercising information analysis and creative thinking, from the presentation of a contextualized problem in the desert, where students had to give a practical use of a series of objects with which the character in the story had so that he could survive until he was rescued.
4. d. The fourth activity consisted in individual and group work, with the aim of developing problem-solving skills based on information analysis, creative thinking, and experimentation; that is, four contextualized arithmetic problems were proposed, which were put into practice with material so that the students could solve them in a concrete way.
5. e. The fifth activity involved individual, team and group work, with the aim of developing problem-solving skills based on information analysis, creative thinking, and dialogue. Two contextualized arithmetic problems and a logical reasoning exercise were proposed, which were solved individually, once the students were finished, they met in teams to compare their answers and a space for dialogue was opened between the teams to discuss which the results were and how they were reached.
6. f. In the sixth activity, we worked again at the individual, team and group level, with the aim of developing problem-solving skills based on information analysis, creative thinking, dialogue and consensus. Two contextualized arithmetic problems were proposed, a logical reasoning exercise and a generalization exercise, which at the choice of each student could be solved individually, in teams and / or using some material (concrete or abstract). After solving each problem, a space for exchanging ideas was held about what the results were and how they were reached.
7. g. The seventh activity consisted of closing the intervention through orderly participation and the exchange of ideas about the importance and significance of solving problems from the arithmetic and logical point of view in a familiar and daily context to the life of each student.

In the ninth session, the final evaluation was applied with the proposed instrument, gathering information on how to solve contextualized arithmetic problems.

The sociodemographic data of the participants show that the mean age is 11.0 years, likewise the distribution by sex was 31 men and 30 women. Likewise, it was found that 75% of the participants reside in the same neighborhood where the school is located, 24% live in neighboring neighborhoods and only 1% live in an area far from the school. n the analysis of the responses for each problem per student, a frequency distribution was made, which as seen in Figure 1 and 2 shows the performance of the students at the time of solving each contextualized arithmetic problem in the initial evaluation (pre-test) and final (post-test) respectively.

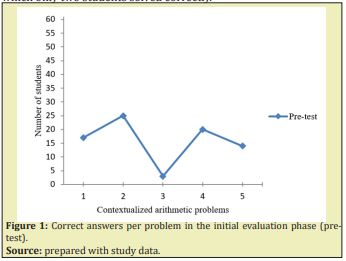
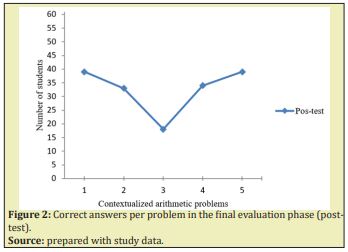
Figure 1 shows the performance of the students before the five problems proposed in the initial evaluation, the second being the most solved correctly by 25 students, and the third problem in which only two students solved correctly.

In Figure 2, under the use of the same instrument, the performance of the students is observed in the face of the five problems proposed in the final evaluation, the third problem being the one that collected the least number of correct answers from the students. While the first and fifth problems were answered correctly by a total of 40 students.

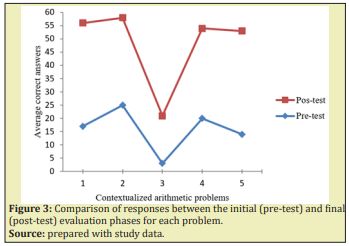
For the analysis between the pre-test and post-test conditions per problem (Figure 3), a one-way Analysis of Variance was performed where no statistically significant differences were observed (F(4,4)=5.215, *p=<.05). As the performance lines between the initial and final evaluation conditions are appreciated, a statistical significance is not achieved given the impoverishment of correct responses to the third problem.

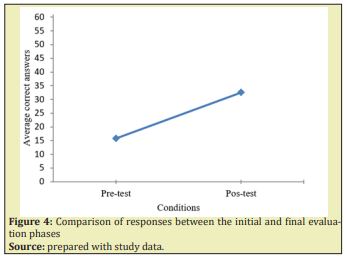
In the comparison analysis between the pre-test and post-test conditions (Figure 4), a one-factor Analysis of Variance was applied in which it was observed that the performance between the pre-test and post-test conditions did not reach a statistically significant level (F(1,4)= 30.880, **p= < .01), since, as can be seen, despite the considerable increase in the average of correct answers, it does not exceed the level of chance.

In the final part of the instrument, three open questions were applied in which the students had to answer aspects of their experience and perception of the intervention carried out. The responses were analyzed based on semantics and frequency of appearance.

In the first question where they were asked about their prior knowledge before the intervention, 39 % (N=24) of students stated that they knew in advance the basic arithmetic operations (e.g. Addition, subtraction, multiplication and division). Similarly, 10% of the students reported knowing the arithmetic problems (e.g. They always have a question; you must answer them with an operation).

Faced with the following question about the knowledge acquired during the intervention, the students' responses were basically grouped into three axes. In the first, some cognitive process was explicitly reported (e.g. I learned to solve problems, I learned more, I understood the context, reflect on the problem, reflect on the answer, better understand arithmetic operations, understand what I read), alluding to the self-referential ability that students have in learning moments (N=18). The second response axis made up of 12 cases, the students answered about problem solving (e.g. solve problems in an easier way; that all problems have information, data and a result is expected; solve problems all the time not only at school). In the third axis the students (N=10) stated that they acquired knowledge about arithmetic operations (e.g. Multiply and divide; use arithmetic operations elsewhere; I got better doing addition, subtraction, multiplication and division).

Finally, in the third question, the generalization of contextualized problem solving was investigated, where with 49 cases (80%) the students reported that the content addressed in the intervention would be useful in activities of their daily life (e.g. When I buy, when I have to pay, when I get on the truck, because the mathematics is the games, in the music, when playing an instrument, to save money).

Although the discursive results described here are not directly related to the resolution of the contextualized arithmetic problems proposed in the instrument used in the initial and final evaluation, they do contribute to obtaining an overview between the moments prior to the test, during the intervention and on the use of developed skills.

Mathematical ability consists of the acquisition of the skills to apply with precision and rigor the knowledge and mathematical reasoning in the description of reality and in solving problems in everyday life;⁴ however, in order to achieve this, basic skills must be developed such as counting, handling large and precise numbers, mental numerical representation and the geometric notion.^2,3 Arithmetic is an area of mathematics classified as one of the most basic, based on four axioms that are: addition, subtraction, multiplication and division; In order to access the method of use of arithmetic knowledge, the problems to be solved were raised^19,20 where the results showed the differences between the pre-test and post-test conditions.

As shown in Figure 1, the performance levels that the students had as a problem are poor, that is, the correct way of solving was very poor, which indicates that the students solved the problems mechanically using the known algorithms, without previously analyze the context.^19-22

Based on the above, an aspect that was observed among the students, and that explains the impoverished performance that they obtained in the initial evaluation, is a function of school practices that have already been normalized, such as repeating response patterns guided by the memory⁹ applying any arithmetic operation that they consider convenient or that they know best.

For its part, despite not having the numerical parameters to accept a statistically significant difference in performance between the conditions, what is observed (see Figure 3) is that there is a pattern of improvement in the resolution task, which is consistent with the data reported by Martínez and collaborators.¹⁹

The differences in the levels of execution by problem and between phases, offer a reading that, although statistical significance was not achieved, which would contribute to the evidence on a consolidation of the style of thought²³ and the structuring and incorporation of the principles of the PBL, if a point was reached where the student was able to improve their performance in solving problems and self-reflection expressed through their discourse on the information addressed in the intervention.

The PBL, as already mentioned, is a pedagogical tool used mainly in the population segments of upper secondary education onwards,^9-14,16-18 however, given the results obtained, one can have a certainty that basic level students, specifically sixth grade students, can acquire and develop certain cognitive skills, aptitudes and attitudes towards knowledge of arithmetic problem solving through PBL.

The PBL when formulated from a constructivist approach, seeks that the student can create a relationship with the object,^12,13 therefore, in the proposed intervention strategy, half of the problems were taken to experimentation^12,13 and approached from concrete thinking tools,^5,8 this represents an aspect that could generate differentiation in the resolution of contextualized problems before and after the intervention and an explanation is found in which students can give a better response to a problem raised when its contextualization is established (object of study of the present investigation) and from its location, situation and material used.²⁴

Also, it was observed that students implement the elements of the ABP such as analysis, solution and small group discussion of some problems^10,11 were able to identify very specific daily life activities that explicitly reported verbally that the knowledge learned would serve them in such situations.

Although the main objective of the PBL is the integral development of the student, that is, to combine the acquisition of knowledge with skills, attitudes and values¹³ faced with the contents of the intervention and the perception of the students' own learning, it is shown that while working on a set of skills, it is also done from the transformative point of view in the subject of mathematics,^12-18 because students discursively and attitude at the beginning of the intervention showed resistance and little interest to the content, to the closure of nine sessions not only showed learning about solving arithmetic problems contextualized but were interested to observe what activities daily used this knowledge, data that is consistent with the results obtained by Martínez and collaborators.¹⁹

The Problem-Based Learning methodology is primarily about an integrative, activity-based approach that encourages reflection, complex thinking, cooperation, and decision-making;^9-12,20 therefore, the importance of its application in the basic levels of education falls first in the training and learning styles, study plans and programs and in the stages of cognitive development.

The findings of the study point to being able to obtain empirical evidence on the relevance of the use of PBL in students of basic primary education. In accordance with the literature^12-18 the feasibility of incorporating PBL in the teaching-learning process of the mathematics subject is supported. Likewise, the results of both the performance in solving contextualized arithmetic problems and in the discursive reports obtained by the students are similar to those reported by Martínez and collaborators,¹⁹ however they were achieved in less time.

For its part, the way of solving contextualized arithmetic problems with initial unknowns was poorly resolved when the unknown was placed at the end, which provides a new problem that could be addressed in subsequent studies.

Some of the limitations of the study were a function of the number of students who participated in the intervention, since the participation and availability of the total population of the sixth grade of primary school was not counted on.

Therefore, it is concluded that a first approach to the phenomenon of contextualized arithmetic problem solving was achieved through PBL in sixth grade primary school students; Likewise, an intervention was proposed based on the principles of PBL and the resolution of arithmetic problems in combination with a relevant temporality of application within the natural educational scenario. Although there were no statistically significant differences, the performances between the phases before and after the intervention, adding the verbal responses by the students indicate a change in the construction of knowledge in the resolution of contextualized problems.

None.

None.

Author declares that there is no conflict of interest.

1. 1. Spelk E. Core knowledge. American Psychologist. 2000;55(11):1233–1243.
2. 2. Spelke ES, Gilmore CK, McCarthy S. Kindergarten children’s sensitivity to geometry in maps. Developmental Science. 2011;14:809–821.
3. 3. Huang Y, Spelke ES. (Core knowledge and the emergence of symbols: The case of maps. Journal of Cognition and Development. 2015;16:81–96.
4. 4. Berch D. Making sense of number sense: implications of children with mathematical disabilities. Journal of Learning Disabilities. 2005;1:333–339.
5. 5. Carr M, Alexeev N. Fluency, Accuracy, and Gender Predict Developmental Trajectories of Arithmetic Strategies. Journal of Educational Psychology. 2011;3(103):617–631.
6. 6. Santoyo C. Alternativas Docentes. In: Santoyo C (Ed.), Análisis y evaluación de habilidades metodológicas, conceptuales y profesionales en la formación del psicólogo, (2), México: PAPIME, Facultad de Psicología, UNAM. 2005.
7. 7. Riveros H. La Prueba PISA de la OCDE. Instituto de Física,UNAM, 2007; p. 1–3.
8. 8. Díaz-Barriga F. Aprendizaje Basado en Problemas, de la Teoría a la Práctica. Perfiles Educativos. 2005;28(11):124–127.
9. 9. González E, García L, Blanco A, et al. Aprendizaje basado en la resolución de problemas: una experiencia práctica. Educación Médica. 2010;13(1):15–24.
10. 10. Guevara G. Aprendizaje Basado en Problemas como técnica didáctica para la enseñanza del tema de la recursividad. Revista de las Sedes Regionales. 2010;20(11):142–167.
11. 11. González M, Castro A. Impacto del ABP en el desarrollo de la habilidad para formular preguntas de aprendizaje en estudiantes universitarios. Revista de Docencia Universitaria. 2011;1(9):57–66.
12. 12. Castaño V, Montante M. El método del aprendizaje basado en problemas como una herramienta para la enseñanza de las matemáticas. Revista Iberoamericana para la Investigación y el Desarrollo Educativo. 2015;11(6):1–12.
13. 13. Cazzola M. Problem-based learning and mathematics: posible synergical actions. In: Gómez L, Martí D, Torres  C (editors.), ICERI2008 Proceeding, IATED International Association of Technology, Education and Development, Valencia, España, 2008.
14. 14. Kyeong R. Problem-based learning in mathematics. Clearinghouse for Sciencie, Mathematics, and Evironmental Education. 2013, p.1–3.
15. 15. Lee K. Online collaborative case study learning. Journal of College Reading and Learning. 2007;37(2):82–100.
16. 16. Xiaogang X, Chuanhan L, Bingyi W. Research on mathematics instruction Experiment Based Problem Posing. Journal of Mathematics Education. 2008;1(1):153–163.
17. 17. Sahid S. Mathematics Problem Solving and Problem-Based Learning for Joyful Learning in Primary Mathematics Instruction. Department of Mathematics Education, Yogyakarta State University, 2011.
18. 18. Sengül S, Katranci Y. Structured problem posing cases of prospective mathematics teachers: experiences and suggestions. International Journal on New Trends in Education and Their Implications. 2014;4(5):190–204.
19. 19. Martínez M, Da Valle N, Zolkower B, et al. Los contextos “realistas” en la solución de problemas de matemática: Una experiencia para capacitadores, docentes y alumnos. Grupo Patagónico de Didáctica de la Matemática. 2009; 30–45.
20. 20. Díaz J, Bermejo V. Nivel de abstracción de los problemas aritméticos en alumnos urbanos y rurales. Revista Latinoamericana de Investigación en Matemática Educativa. 2010;10(3):335–364.
21. 21. Verschaffel L, de Corte E, Lasure S. Realistic considerations in mathematical modeling of school arithmetic word problems. Learning and Instruction. 1994;4:273–294.
22. 22. Vicente S, Van Dooren W, Verschaffel L. Utilizar las matemáticas para resolver problemas reales. Cultura y Educación. 2009;20(4):391–406.
23. 23. MacMath S, Wallace J, Chi X. Problem-based learning in mathematics, A tool for developing students´ conceptual knowledge. What Works? Research into Practice. 2009:22:1–4.
24. 24. De Franco T, Curcio F. A division problem with a remainder embedded across two contexts: Children´s solutions in restrictive versus real-world settings. Focus on Learning Problems in Mathematics. 1997;19 (2):58–72.