To unify gravitational interaction with other three kinds of interaction are a work hadn’t been finished by Albert Einstein and a big problem that human must solve to continue living in the universe. As the covariant derivative in gravitational theory, i.e., in general relativity has similar structure to that in gauge theory, (it is worth mentioning that for the covariant derivative for a covariant vector), people asked whether there would some links between the connection (or for covariant vector) and the graviton, and whether gravity could be described by a gauge theory. Starting from quantum mechanics, the relationship between symmetry and the invariance of the Lagrangian may be the essence of the gauge invariance in gauge theory, which represents the invariance of Lagrangian under a gauge transformation; therefore, a gauge theory of gravity may also be built in a similar way from this relationship by , for which reason the covariant derivative of a tensor must remain to be a tensor as the original tensor , and it leads to the existence of connection or .
The conservation law has theoretical explanation in quantum mechanics. When there is a symmetry, the system, i.e., a state would keep invariant after a transformation which is under this symmetry.
Supposing there is a symmetry, the transformation under this symmetry is , an arbitrary state is , then would be invariant under transformation , that is,
(1)
where is a parameter, and it could be proved that Hamiltonian is therefore also invariant:
(2)
If there is such a symmetry, for arbitrary state
there must be a complete set of the eigenstates of the Hamiltonian
, (3)
That any state could be expanded by this complete set of the Hamiltonian :
(4)
thence
that is (2)
When there is a symmetry and its transformation to any state is , there is always (1) since there is symmetry, this leaves the Hamiltonian also invariant by the transformation under the symmetry, this invariance could be represented as the commutative relation (2) and a conserved quantity could be derived there from.
For example, the conservations of energy and momentum were led by the symmetry when the state was transported in time and space, a state keeps invariant after such a transformation and therefore there is commutative relations between the Hamiltonian and the transformation operators for the transportations. The transformation operator in time and space could be:
(5)
and it could be proved that any function could be expanded as Taylor series:
(6)
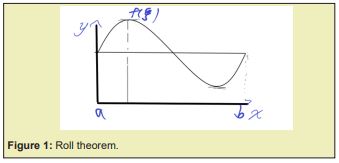
The proof of Taylor formula starts with Cauchy mean value theorem which starts from Roll theorem,
as Figure 1 shows, when there is a continuous function derivable in , there must be a between that has zero derivative there:
(7)
, since there must be at least one extremum point between if . Supposing it is , the right and left derivative at this point satisfies
(8a)
(8b)
when it is minimum, or
(8c)
(8d)
when it is maximum, and since the derivative exists in every point of this region
(9)
where .Lagrange mean value theorem could be proved with Roll’s:
Define Figure 2
(10)
the later part is the just the straight line between points and , then one could apply Roll’s theorem as proved before, there must be a point between where, that is
, (11)
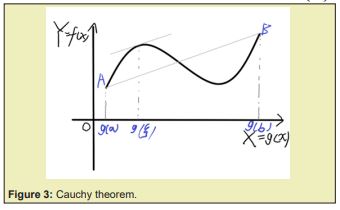
(11) is the Lagrange mean value theorem. Cauchy mean value theorem is one more step after Lagrange’s, and are two functions of variable , define:
, ,
as shown in Figure 3, there must be a point that makes:
(12)
that is
(13)
where (13) is Cauchy mean value theorem. Using Cauchy’s mean value theorem could prove that any function could be expanded as Taylor series:
(14)
where could be proved to be and
Applying Cauchy mean value theorem
the four-dimensional momentum is a conserved quantity, this conservation comes from the symmetry when the system was transported in space and time. And since is a conserved quantity, the effect of this transformation to any state would be , and this is just to add a phase to the state, and the state keeps invariant under the transformation.
In gauge theory for the electromagnetic interaction, the system, i.e., a stateof electromagnetic field, must keep invariant under a transformation:
(28)
because of the conservation of electric charge and gauge invariance, it is required that:
(29)
which is to remain the Lagrangian invariant, because the transformation doesn’t change the coordinate in .This invariance could be from a symmetry in the field, of which the transformation under this symmetry is , and the state keeps invariant after a transformation under this symmetry:
(30)
.This requires that the Lagrangian (Lagrangian and Hamiltonian same represent the energy of the system, as a function of only , where and are general coordinates and momentums respectively, ) must keep invariant after a transformation, therefore there must be
(31)
whereis a conserved quantity since for the symmetry as well. This is electric charge conservation, and the transformation would be:
(32)
where is the value of the conserved quantity of the state, and since the Lagrangian consists of only , i.e., , and it is after quantization, since , , then (31) would lead to
(33)
this is exactly (29), the gauge invariance after a gauge transformation in the gauge field for electromagnetic interaction, it is because of a symmetry, i.e., , under which the transformation operator is , and it is the reason for the conservation of electric charge.
In summary, the gauge invariance in electromagnetic field originates from a symmetry, and the transformation under this symmetry keeps the system invariant, such a transformation is a gauge transformation, and the transformation must keep the Lagrangian invariant. This invariance leads to (31), which is equivalent to:
(34)
where for the conservation of electric charge, led by that the transformation keeps the Hamiltonian invariant (31), and this is exactly (29) in the gauge theory for the electromagnetic field, it represents the invariance of the Lagrangiansame as (31).
Moreover, usually the factor in the gauge transformation (30) is local, not global anymore, that is, would be a function of ,i.e., and not a parameter anymore, but the Lagrangian still keeps invariant under the transformation, therefore there could be a modification to the partial derivative:
(35)
to keep
(36)
still equivalent to (31) as (33) did when the was global. The Lagrangian must keep invariant as (31) represented because of the symmetry the transformation was under, and is called the covariant derivative in the gauge theory for the electromagnetic field.
By calculating, when there is (35), there must be:
and in is the photon which is the gauge particle of the gauge field for electromagnetic interaction.
The structure of covariant derivative in general relativity,
(36)
is similar to that in gauge theory, and the connections and therein also have similar properties as in , which is the covariant derivative of the gauge field for electromagnetic field, they keep still a tensor after exerted on a tensor in the gravitational field, which should be a state therein.
Historically, people asked whether such a connection may at least have some links with the graviton, the gauge particle of the gauge field for gravitational interaction, it is also what the gravitational wave consists of. According to the relationship between symmetry and the gauge invariance as shown before, this invariance should also be led by a symmetry in the gravitational field which leaves any state in the field invariant after a transformation under this symmetry, and the relation for the invariance of the state (2), should still be similar to (31) and result in a similar relation as (36) between the transformation and the state in gravitational field, supposing such a transformation is ,
(37)
which is equivalent to the invariance of the Lagrangian,
(38)
as (31), and this invariance requires that must still be a tensor as to enable
(39)
where is a parameter, because there must be for the symmetry.
The counterpart quantity to electric charge in electromagnetic field is massin gravitational field, and mass is a combination of energy and momentum according to relativistic mechanics:
(40)
the symmetry that keeps the mass conserved is probably still the transportation symmetry in the conservations of energy and momentum as (22) represented, a state is invariant when it was parallel transported in the space time, and the transformation operator is still
(41)
in (21), as proved before, and the invariance of the state after the transformation leads to
(42)
and it leaves the four-dimensional momentum conserved, therefore , where is the value
of the conserved quantity , and the relation would be
(43)
If a state in the gravitational field is, then (43) is equivalent to
(44)
for Hamiltonian only consists of and their operator are , , this requires that is same a tensor as to make sense of the calculation. When we came to (43), since is not always same a tensor as , we can’t get , but the symmetry demands that there must be (43), so we could construct the covariant derivative (36) in gravitational field to and we could get (44) which is equivalent to (43); therefore, also must still be a tensor as , (44) expresses the invariance of Hamiltonian after the transformation under the transportation symmetry. As Einstein’s gravitational field finally is
(45)
where is the energy-momentum tensor, gravity may also be described by a gauge theory as (44).

Thanks to everyone.
None.
Author declares that there is no conflict of interest.
- 1. Qian Bochu. Quantum Mechanics. Higher Education Press. Beijing.
- 2. Duan Yishi. General relativity and gravitational gauge theory. Science Press. Beijing.
- 3. Yang CN. Gauge invariance in classical field theories. Phy Rep. 1978;9C:1.

